poltfield.blogg.se - Regress y on x

Using the appropriate regression equations, find iii)The level of sales expected next year when 2000 building permits are to be issued. He has accordingly collected the data for the sales (y) and the number of building permits issued (X) in the past 10 years. Large deductions, which include charity and m A furniture retailer in a locality is interested in studying whether some relationship exists between the number of building permits issued in that locality in the past years and the volume of sales in those years. To the Internal Revenue Service, the reasonableness of total itemized deduction depends on taxpayer’s adjusted gross income. ii)The level of sales expected next year when 2000 building permits are to be issued.ģ. Using the appropriate regression equations, find i)The level of sales expected next year when 2000 building permits are to be issued. He has accordingly collected the data for the sales (y) and the number of building permits issued(X) in the past 10 years. A furniture retailer in a locality is interested in studying whether some relationship exists between the number of building permits issued in that locality in the past years and the volume of sales in those years. Regression equations of Y on X and X on Y.Ģ.

A computer while calculating correlation coefficient between two variables X and Y from 25 pairs of observations obtained the followingįind the correlation coefficient of X and Y. For example, in the correlation of heights of fathers and sons, a tendency of human race to return to or regress to the average height is observed.ġ.

The meaning of regression is a tendency of returning to the mean. The functional relation between the variables is called as regression equation.

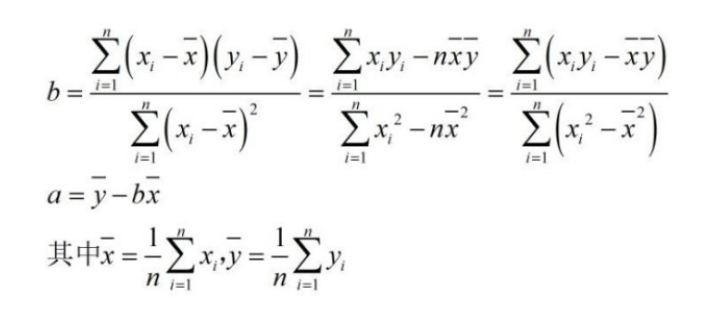
We derive the equation that defines the relationship, which is linear, as we have defined linear correlation in the previous sections. If the relationship is established and is significant then next step is to obtain the expression of relationship of the variables. Coefficient of correlation gives the magnitude of the association of two variables. We know that such relationships are measured using coefficient of correlation. Such kind of analysis is required if the data we have is dependent on each other or have some type of causal relationship. We may be interested in knowing if the demand of a commodity has been in the past then what will be the future demand may be two years later if the same trend continues. Like if price is increased how will demand be affected. In business many a times we want to predict what may happen if some action is taken.

Understand the application of regression analysis in business.

Understand the relation of correlation and regression.

Therefore, $r^2$ for this data set is much smaller than $r^2$ for the data set in (a).įigure 8.12 - The data in (a) results in a high value of $r^2$, while the data shown in (b) results in a low value of $r^2$.įor the data in Example 8.31, find the coefficient of determination.After reading this chapter, you are expected to learn about: On the other hand, for the data shown in (b), a lot of variation in $y$ is left unexplained by the regression model. \textrm$'s are relatively close to the $y_i$'s, so $r^2$ is close to $1$. First, we take expectation from both sides to obtain Where $\epsilon$ is a $N(0,\sigma^2)$ random variable independent of $X$. Here, we assume that $x_i$'s are observed values of a random variable $X$.